Write a C program to find the root of equation using Newton Raphson Method. Equation: 2x^3-6x^2+6x-1

In this C program we will find the root of equation using Newton Raphson Method. The equation is: 2x^3-6x^2+6x-1
The allowed error is: 0.001

Introduction:

Introduction:From NewtonRaphson Method we know, Xn+1=Xn-[f(x)/f'(x)].
Here we consider three functions one to generate the given equation, other to generate the derivative of the given equation. And the other to find out the root of the equation by using Newton Raphson Method. For this here we passes two values given by the users.

input:

a and b, two arbitrary values will be given by the user.

output:

The root of the equation.

CODE---->

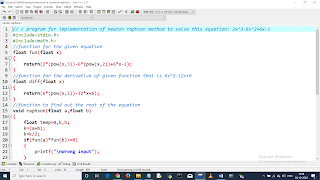
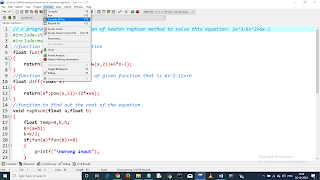
// c program for implementation of newton raphson method to solve this equation: 2x^3-6x^2+6x-1
#include<stdio.h>
#include<math.h>
//function for the given equation
float fun(float x)
{
	return(2*(pow(x,3))-6*(pow(x,2))+6*x-1);
}
//function for the derivative of given function that is 6x^2-12x+6
float diff(float x)
{
	return(6*(pow(x,2))-12*x+6);
}
//function to find out the root of the equation
void raphson(float a,float b)
{
	float temp=0,k,h;
	k=(a+b);
	k=k/2;
	if(fun(a)*fun(b)>=0)
	{
		printf("\nWrong input");
	}
	else
	{
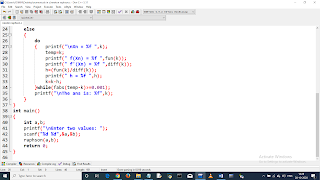
		do
		{   printf("\nXn = %f ",k);
			temp=k;
			printf(" f(Xn) = %f ",fun(k));
			printf(" f'(Xn) = %f ",diff(k));
			h=(fun(k)/diff(k));
			printf(" h = %f ",h);
			k=k-h;
		}while(fabs(temp-k)>=0.001);
		printf("\nThe ans is: %f",k);
	}
}
int main()
{   
	int a,b;
	printf("\nEnter two values: ");
	scanf("%d %d",&a,&b);
	raphson(a,b);
	return 0;
}

Download the C-Program file of this Program.
Download the MS-Word file of this whole assignment with algorithm.

Don't just read, run on your pc !!!

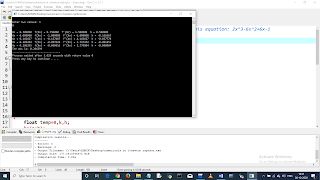
RESULT :

Enter two values: 1
0

Xn = 0.500000  f(Xn) = 0.750000  f'(Xn) = 1.500000  h = 0.500000
Xn = 0.000000  f(Xn) = -1.000000  f'(Xn) = 6.000000  h = -0.166667
Xn = 0.166667  f(Xn) = -0.157407  f'(Xn) = 4.166667  h = -0.037778
Xn = 0.204444  f(Xn) = -0.007028  f'(Xn) = 3.797452  h = -0.001851
Xn = 0.206295  f(Xn) = -0.000016  f'(Xn) = 3.779804  h = -0.000004
The ans is: 0.206299
--------------------------------
Process exited after 6.369 seconds with return value 0
Press any key to continue . . .

Images for better understanding :

Discussion:

The Newton-Raphson method is an iterative approach to finding the roots of some differentiable function f(x)f(x). The method is advantageous, because it is simple to implement, and when it works, it approaches x∗quadratically and is relatively efficient. Basically, Newton's method works best when applied to find non-repeated roots of a differentiable function, because it guarantees quadratic convergence. It require the derivatives of f(x)), if complicated then this method will tend to fail. It require very accurate initial value or initial guess Xo. Must be near the root you need to approximate.